この文書の URL は http://www.cc.kyoto-su.ac.jp/~mtkg/lecture/comp_B/2012/report2.html です。

レポート問題

以下の問題から3問以上選んで解答せよ。 用いるプログラム言語は Fortran または C とする。 プログラムリストと結果を記した PDF ファイルを Word または TeX で作成し、moodle 上で提出すること。 締め切りは 2/8 (金) とする。

＊＊＊注意＊＊＊

moodle で提出する際は、以下のリンクから moodle 学生用マニュアル（レポートの提出＞「単一ファイルのアップロード課題」を提出する）をよく読んで、ファイルが正しくアップロードされたことを必ず確認してください。 期日までにファイルがアップロードされていない場合は未提出となります。

自宅の Windows パソコンでプログラミングする方法

Windows 用の GNU Fortran が配布されているようです。

Cygwin や仮想環境に Ubuntu をインストールしてもよいですが、やや難易度が高いかもしれません。

問1. 覆面算

次の覆面算の解を求めるプログラムを作成し、実際に解を求めよ。

　　　ゆきおんな
＋）　ゆきおとこ
────────
　　かんけいない

ただし、解は次の条件を満たすものであること。

ヒント： 「違う文字には違う数字」を入れるには、異なる文字の値が同じ場合は cycle 文を使ってループをスキップすればよい。 以下の「バナナ＋バナナ＝シナモン」の例を参考にせよ。

クリックして表示

問2. 二分法

区間 [a, b] で定義される単調増加関数 y = f(x) があり、 f(a) < 0, f(b) > 0 であることがわかっているとする。 このとき、次のような方法で f(x) = 0 の数値解を求めることができる。

このような方法を「二分法」という。

関数 f(x) = x*x-2 を区間 [0, 2] で考えると単調増加である。 二分法で f(x) = 0 の解を求めよ。 解析解は √2 である。

問3. エルミート多項式

n 次のエルミート多項式 Hn(x) を返す関数 hermite(n, x) を作成せよ。 任意の実数 x に対して Hn(x) は次の漸化式で定義される。

H0(x) = 1
H1(x) = 2 * x
Hn(x) = 2 * x * Hn-1(x) - 2 * (n-1) * Hn-2(x)     (n >= 2)

Gnuplot を用いて [-10, 10] の範囲で関数 Hn(x) * exp(-x*x/2) (n=1, 2, 3, 4, 5) を作図せよ。

問4. コッホ曲線

コッホ曲線 (Koch curve) とは「線分を3等分し、分割した2点を頂点とする正三角形を作る」という操作を無限に繰り返すことによって得られるフラクタル図形の一種である（下図）。

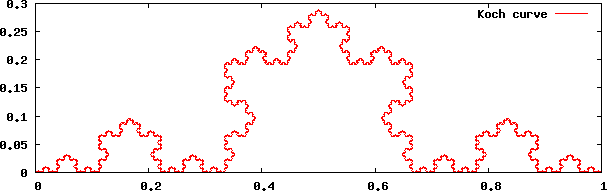コッホ曲線
コッホ曲線

次の説明をよく読み、このコッホ曲線を Gnuplot で作図せよ。

問5. ヒープソート (heapsort)

「ヒープ」と呼ばれるデータ構造を利用した効率のよいソート方法の一種として「ヒープソート」が知られている。 次の説明をよく読み、引数の real(8) 型または double 型配列をヒープソートによって昇順にソートするサブルーチン hsort() を作成せよ。

作成した hsort() を用いて10万個の実数データ random.dat を並べ替え、10番目に小さい値がいくつか調べよ。 random.dat は各行に1つの実数値が書かれた10万行のテキストデータである。

  0.193280739473E+00
  0.501820706178E+00
  0.482727793655E+00
  :
  0.286804437857E+00