ヒープソートとは

数値データを大きさの順に並べかえる方法（アルゴリズム）にはいろいろな種類があるが、 ここでは J. W. J. Williams が考案したヒープソート (heapsort) を紹介する。

  1. ヒープの定義
  2. ヒープソートのオーダー
  3. ヒープの構成方法
  4. ヒープソート
  5. 参考文献

ヒープの定義

ヒープ (heap) とは「どのノード (node) の値も、その直下に位置する2つあるいは1つの子 (child) の値以上である」という順位を持った2分木構造 (binary tree) のことである。 以下にヒープの例を示す。

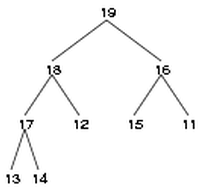図1: ヒープの例
図1: ヒープの例

ヒープの定義により、一番上のノード（ルート, root という）には最も大きな値が入る。

2分木がヒープをなしている場合、これを昇順にソートするには次のようにすればよい。 まず、一番上のノードから最大値を除き、空いた一番上のノードに子のうちの大きい方を上げる。 こうしてできた空ノードに、また子のうちの大きい方を上げる。 以下、ヒープが再構成されるまで同様の操作を繰り返す。 その後、一番上のノードから2番目に大きい値を除き、同じ操作を要素がなくなるまで繰り返せばソートが完了する。

図1の例では、まず 19 を除きそこに 18 を上げる。 18 のあった場所には 17 を上げ、17 のあった場所には 14 を上げる。 以上で1回目の操作が終了する。 以下同様に、18 を除いてヒープを再構成し、17 を除いてヒープを再構成し…、と続けていくわけである。

ヒープソートのオーダー

ソートに必要な時間は、主に大小比較の回数で評価することができ、これはソートする配列の要素数 N の関数として表せる。 ヒープソートの場合、最大値を取り去ってヒープを再構成するのに必要な比較回数は、次のように見積もることができる。 2分木の構造上、1回の大小比較によって次の比較の対象となる要素数は比較前の半分になる。 したがって、ヒープの再構成が終了するまで（つまり、残りの要素数が 1 になるまで）に必要な比較回数 C は

N ≒ 1 + 2 + 2**2 + 2**3 + ... + 2**C  =>  C = log2(N+1) - 1

で与えられる。 N が十分大きければ C はほぼ log2(N) である。 N 個の要素全部をソートするには各要素についてヒープの再構成が必要になるから、全体で必要な比較回数は N*log2(N) 程度になる。 このことを「ヒープソートは O(N log N) のアルゴリズムである」とか、「ヒープソートのオーダーは O(N log N) である」と表現する。

別のソート方法として単純挿入法を考える。 この方法では、まず1番目と2番目の要素を比較し整列する。 次に3番目の要素と先頭の2つの要素を比較し正しいところに挿入する。 以下、同様の操作を繰返し、最後の要素を適当なところに挿入して整列が終る。 このアルゴリズムの場合、必要な比較回数は N(N-1)/2 程度となる。 N が大きい場合には N*N の項が支配的となるので、オーダーは N**2 であり、O(N**2) と表現する。

N*log(N) と N**2 の大きさを比べると、N が大きいときは N*log(N) のほうが圧倒的に小さい。 したがって、N が十分大きい場合には単純挿入法よりもヒープソートのほうが圧倒的に高速である。 同様の高速なアルゴリズムには「クイックソート (quick sort)」などがある。 オーダーはヒープソートと同じく N*log(N) である。

ヒープの構成方法

既に述べたように、2分木がヒープになっていればそれをソートするのは簡単である。 与えられた配列 x(i) を2分木とみなしヒープを構成するには次のようにすればよい。

配列と2分木の対応

まず、配列の添字 (i) と2分木上の位置を図2のように対応させる。

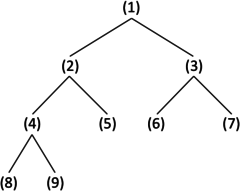図2: 配列の添字と2分木上の位置の対応
図2: 配列の添字と2分木上の位置の対応

これからすぐわかるように i 番目の配列要素の子にあたる配列要素は 2i 番目と 2i+1 番目の配列要素となる。

ヒープの構成

2分木とみなした配列をヒープにするには次のようにする。

ヒープの構成（具体例）

実際にヒープを構成するまでの手順を以下に示す。 配列の長さは 9 とし、初期状態は次のようになっているものとする。

[12, 13, 16, 14, 18, 15, 11, 17, 19]

■ step 1-3

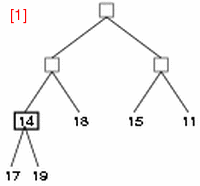
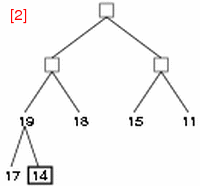
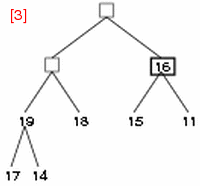
step1の図 step2の図 step3の図

■ step 4-6

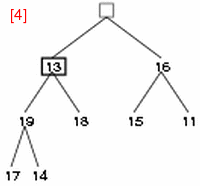
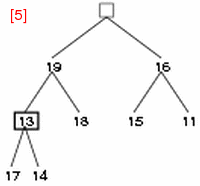
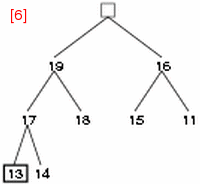
step4の図 step5の図 step6の図

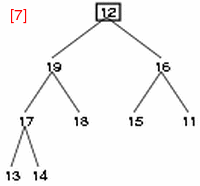
■ step 7-9

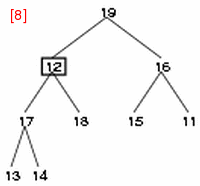
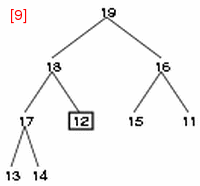
step7の図 step8の図 step9の図

ヒープの構成プログラム

以上のアルゴリズムを Fortran プログラムにすると次のようになる。

!
! 整数の配列 x(i) をヒープに変換するプログラム
!
program main
  implicit none
  integer, parameter :: nmax = 9
  integer :: x(1:nmax) = (/ 12, 13, 16, 14, 18, 15, 11, 17, 19 /)

  integer :: i, j, n, tmp
  character(len=*), parameter :: fmtx = '(9I5)'
  logical :: debug = .true.

  write(*,fmtx) x(1:nmax)

  ! 配列の前半部分の最後 [14] から始める。
  ! 要素数が 2 で割り切れない場合も nmax/2 から開始すれば OK。
  do n = nmax/2, 1, -1

     ! 以下、x(n) を適当なところまでふるい落とす。
     tmp = x(n)

     ! まず直下の子から比較していく
     i = n
     j = i * 2                  ! j は2分木上の左下の子の添字

     ! ふるい落としのための DO ループ
     do
        if (j > nmax) exit      ! 子がなくなったら終了

        ! 子が2つある場合は、大きい方を x(j) とする。
        if (j < nmax) then
           if ( x(j+1) > x(j) ) j = j + 1
        end if

        ! * 子の方が大きければ x(j) を x(i) に上げた後
        !   i = j, j = i * 2 として処理を繰り返す。
        ! * 子の方が小さければふるい落しは完了なので
        !   j = nmax + 1 として DO ループから抜ける。
        if ( x(j) > tmp ) then
           x(i) = x(j)
           ! debug = .true. の時は途中経過を表示
           if ( debug ) then
              x(j) = tmp
              write(*,'(I3,A,I3)') x(j), ' <=> ', x(i)
              write(*,fmtx) x(1:nmax)
           end if
           i = j                ! 下のノードに移る
           j = i * 2
        else
           j = nmax + 1         ! 子の方が小さいのでふるい落とし完了
        end if
     end do

     ! x(n) をふるい落した先に代入して次の要素へ移る。
     x(i) = tmp
  end do

  ! 結果表示
  write(*,fmtx) x(1:nmax)

  stop
end program main

ヒープソート

配列をヒープにできたらソートを行なう。 これはヒープを構成するアルゴリズムを少し修正することで簡単に行なうことができる。

  1. ヒープの一番上のノード (root) にある要素（配列の先頭）と、最も右下にある葉（配列の末尾）にある要素を入れ換える。この時点で配列の末尾に最大値が入るので、ヒープの要素からはずす。
  2. 葉にあった要素を root に移動したのでヒープは乱れてしまっている。root に移動した要素をふるい落としてヒープを再構成する。
  3. ヒープが空になるまで 1, 2 を繰返す。終了した時点で配列全体のソートが完了する。

実装例

自分でプログラムを作ってみて、どうしても動かなかったら参考にすること。

参考文献