問題1〜4から2問以上,問題5〜8から2問以上選んで解答せよ. 最終回の講義 (1/14) までに高木のチェックを受けて OK をもらうこと.
素数の判定
キーボードから入力した数が素数かどうか調べるプログラムを作成せよ.
ヒント: 2以外の偶数は素数ではない. 奇数が素数であるかは,次のようにして判定できる.
- k = 3, 5, 7, ..., n-2 に対して n が k で割り切れるか調べる.
- 途中で割り切れれば素数でない.
- すべての k に対して割り切れなければ素数である.
数当てゲーム
適当な数を入れると,正解よりも大きいか,小さいか,または正解であるかを出力する. それを繰り返すことで答えを探すことができる. このゲームを作成せよ. 答えの正解は乱数を使って毎回別の数字を用意すること. 乱数の使い方は次のプログラムを参考にせよ.
!----------------------------------------------------------------- ! 乱数のサンプルプログラム !----------------------------------------------------------------- program random_example implicit none integer :: n, i, clock, secret integer, allocatable :: seed(:) real :: r ! 初期化用配列を取得 call random_seed(size=n) allocate(seed(n)) ! システムの時刻を取得 call system_clock(count=clock) ! システムの時計を使って乱数列を初期化 seed(1:n) = clock + 37 * (/ (i-1, i=1, n) /) call random_seed(put=seed) ! 整数 secret の設定 (0 < secret < 10000) do call random_number(r) ! r には 0 < r < 1 の乱数がセットされる secret = int(r * 10000) ! r を 10000 倍して整数部を secret にセット if (secret > 0) exit end do write(*,*) secret stop end program random_example
乱数の初期化方法については以下のサンプルプログラムが参考になる.
ラゲール多項式
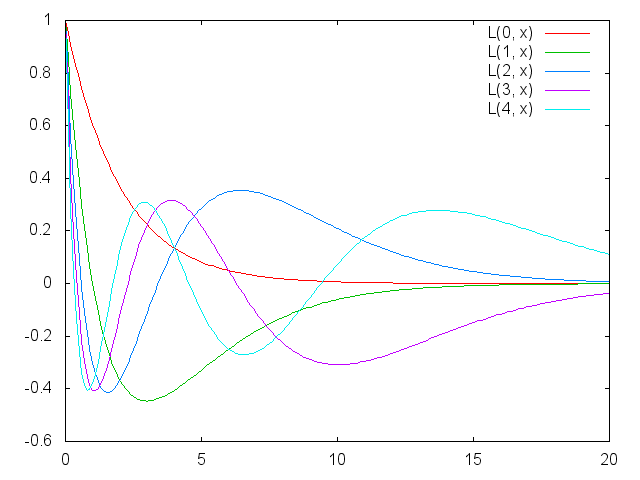
n 次のラゲール多項式 (Laguerre polynomials) L(n, x) は次の漸化式で定義される.
L(0,x) = 1 L(1,x) = 1 - x n * L(n,x) = (2*n-1-x) * L(n-1,x) - (n-1) * L(n-2,x) (n >= 2)
n = 0, 1, 2, 3, 4 に対して
exp(-x/2) * Ln(x)
のグラフを Gnuplot で図示し,n 次のラゲール多項式は n 個の零点を持つことを確かめよ. x の範囲は [0, 20] とする. 次のようなグラフが得られれば OK.
多数桁計算
「整数÷整数」の計算を小数の任意の桁まで行う以下のプログラムを完成させよ. 2つの整数 a, b と桁数 n はキーボードから入力する. ただし、桁数の上限はあらかじめ決めておいてよい(以下のヒントでは 1000 としている). 例えば,20÷17=1.7647… の結果は次のように表示される.
% ./a.out
Input a, b
20 17
How many digits?
100
1 .
76470 58823 52941 17647 05882 35294 11764 70588 23529 41176
47058 82352 94117 64705 88235 29411 76470 58823 52941 17647
05882 35294 11764 70588 23529 41176 47058 82352 94117 64705
88235 29411 76470 58823 52941 17647 05882 35294 11764 70588
ヒント: 筆算をプログラムに直せばよい. 商の整数部を表す整数 p と小数部を表す整数配列 q(:) を用意し,手順をループで表現する.
!------------------------------------------------------------ ! 多数桁計算: a / b を小数 n 桁まで計算する ! 計算方法は筆算をプログラムに直すだけ. ! ! nmax 桁数の最大 ! p 商の整数部 ! q(i) 商の小数部, q(i) は商の小数第 i 桁を表す !------------------------------------------------------------ program muldiv implicit none integer, parameter :: nmax = 10000 integer :: a, b, n, p, q(nmax) integer :: i write(*,*) 'Input a, b' read(*,*) a, b write(*,*) 'How many digits?' read(*,*) n if (n > nmax) then write(*,*) 'Too many digits! N must be <= ', nmax stop endif ! 整数部: p p = a / b ! 商 a = a - p * b ! 余り ! 小数第 i 桁: q(i) do i = 1, n !***************************************************************** ! この部分を自分で考える !***************************************************************** end do ! 結果表示 write(*,*) p, '.' write(*,'(10(1X,5I1))') q(1:n) stop end program muldiv
双子素数
1 から n までの間の双子素数(差が 2 であるような素数の組)をすべて求めよ. n はキーボードから入力できるようすること. 双子素数の例には,3 と 5,5 と 7,11 と 13,…,857 と 859 などがある.
以下に 1000 以下の双子素数を探した結果を示す.
% ./a.out
3 5
5 7
11 13
17 19
: :
857 859
881 883
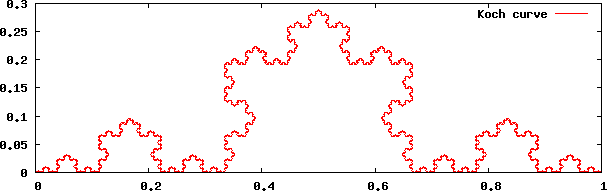
コッホ曲線
以下の解説を参考に,Gnuplot でコッホ曲線を作図するプログラムを作成せよ.
コッホ曲線は次のようなフラクタル図形の一種である.
多数桁計算(Napier 数)
自然対数の底 e (Napier 数)を任意の桁数(小数第 K 位)まで計算するプログラムを作成せよ. Napier 数の求め方は以下の通り(京大冨田先生の解説より).
e = 1 + 1/1! + 1/2! + 1/3! + 1/4! + ... [exp(x) の x=1 でのテイラー展開]
を次のように変形する.
1 1 1 1 1
e = 1 + - (1 + - (1 + - (1 + ... --- (1 + -) ...)))
1 2 3 M-1 M
小数第 K 位までの多数桁小数を考え,「多数桁小数÷整数」の計算を次のように繰り返す.
- 十分大きな整数 M に対して 1.000…0 / M を計算し,1 を加える. (最初の多数桁小数は,整数部が 1,小数部がすべて 0 とする)
- その結果を M-1 で割り,1 を加える.
- その結果を M-2 で割り,1 を加える.
- …
- その結果を 2 で割り,1 を加える.
- その結果を 1 で割り,1 を加える.
このようにして任意の精度で e が求められる. 小数第 K 位まで求める場合,M は M > K*log(10.0) であれば十分である. 例えば K=100 桁の計算をするには K*log(10.0) = 230.25… より M=231 とすればよい.
以下に,e を小数点以下 200 桁まで求めた結果を示す.
% ./a.out How many digits (<= 1000 ) 200 2. 71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274 27466 39193 20030 59921 81741 35966 29043 57290 03342 95260 59563 07381 32328 62794 34907 63233 82988 07531 95251 01901
組み合わせ
n 個の整数 (1, 2, .., n) から r 個の整数を取り出す方法は nCr 通りある. 例えば,n = 4, r = 2 の場合は次の 6 通りである.
(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)
キーボードから n と r を入力し,すべての組み合わせを出力するプログラムを作成せよ.
以下に,n = 5, r = 3 の計算例を示す.
% ./a.out
Input N and R:
5 3
1 2 3
1 2 4
1 3 4
2 3 4
1 2 5
1 3 5
2 3 5
1 4 5
2 4 5
3 4 5

