コッホ曲線

コッホ曲線とは

コッホ曲線 (Koch curve) とは，

線分を3等分し，分割した2点を頂点とする正三角形を作る

という操作を無限に繰り返すことによって得られる，フラクタル図形の一種である．図1に原点 (0, 0) と点 (1, 0) を結ぶ線分から作成したコッホ曲線を示す．

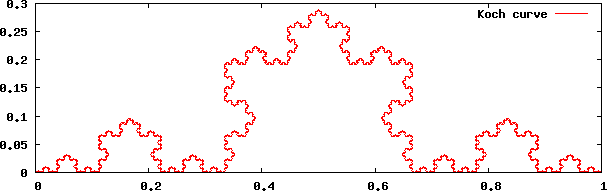図1: コッホ曲線

点 P0 と P1 を結ぶ線分 [P0, P1] からコッホ曲線を作成するには次のような操作を行う．まず，1回目の操作では線分 (P0, P1) に対して点 Q0, Q1, Q2 を次のように定める（図2）．

Q0: 線分 [P0, P1] を 1:2 に内分する点
Q2: 線分 [P0, P1] を 2:1 に内分する点
Q1: Q0 を中心に Q2 を反時計回りに 60 度回転させて得られる点（有向線分 [P0, P1] の「左側」に正三角形 Q0, Q1, Q2 ができるように Q1 を置く）

元の点 P0, P1 と新しい点 Q0, Q1, Q2 を結ぶことにより1回目の操作が完了する．同じ操作を4つの線分 [P0, Q0], [Q0, Q1], [Q1, Q2], [Q2, P1] に対して行うと，さらに複雑な図形が得られる．この操作を無限に繰り返すことによりコッホ曲線が得られる．作図方法からわかるように，1回の分割操作で線分の長さが 4/3 倍になるので，コッホ曲線は無限の長さを持つ．もちろん，分割を無限に続けることは不可能なので，実際に作図する場合にはある程度細かくなったところで分割を打ち切る必要がある．

図2: コッホ曲線の作図方法

2つの頂点 P0, Q0 や Q0, Q1 の間に含まれるコッホ曲線の一部分は P0, P1 の間に含まれるコッホ曲線全体と相似になっている．もっと小さな区間にも全体と相似な図形が存在し，コッホ曲線には全体と相似な図形が無数に含まれる．このような性質を「自己相似」という．

再帰手続き koch() の作成

このコッホ曲線をプログラムで作図することを考える．以下の方針に従って，コッホ曲線の頂点の座標を出力する再帰手続き koch() を作成する．

koch() は P0 と P1 の座標 (p1, p1) を引数として受け取る． p1, p2 は要素数 2 の配列である．
2点 P0, P1 の距離がしきい値 EPS 未満の場合は分割を打ち切り，始点 P0 の座標を画面に出力して return する．
2点 P0, P1 の距離がしきい値 EPS 以上の場合は分割を行う． Q0, Q1, Q2 の座標を計算し，4つの線分 [P0, Q0], [Q0, Q1], [Q1, Q2], [Q2, P1] に対して koch() を再帰呼び出しする．

関数 koch() を始点 P0 (0, 0) と終点 P1 (1, 0) に対して実行すると，図1に示したコッホ曲線の各頂点の座標リストが得られる（EPS は 0.002 とした）．また，koch() は終点の座標を出力しないので，一番最後に終点 P1 の座標を出力する必要がある．

以下にプログラムのアウトラインを示す．

クリックして表示

!------------------------------------------------------------
! Koch 曲線のための副プログラム
! -----------------------------
! koch() は2点 P0, P1 の座標を受け取り，次のような処理を行う．
!
! (1) P0, P1 間の距離が十分小さい（しきい値 EPS 未満）場合，
!   始点 P0 の座標を画面に出力して return する．
!
! (2) そうではない場合，点 Q0, Q1, Q2 の座標を求め，4つの始点
!   と終点の組 (P0, Q0), (Q0, Q1), (Q1, Q2), (Q2, P1) に対し
!   て再帰的に koch() を呼び出す．
!
! 点 Q0, Q1, Q2 は次のように定義する．
!
!  - Q0 = P0 + DX
!  - Q2 = Q0 + DX
!  - Q1 = P0 + (R60 . DX)
!
! ここで，DP は P0 から P1 へのベクトル [P0, P1] を 1/3 した
! もの
!
!  - DX = [P0, P1] / 3
!
! とし，R60 は反時計回りに60度の回転行列とする．
!------------------------------------------------------------
recursive subroutine koch(p0, p1)
  implicit none
  real(8), intent(IN) ::        &
       & p0(1:2),               & ! 始点の座標
       & p1(1:2)                  ! 終点の座標
  ! 以下，ローカル変数
  real(8) ::                    &
       & dist,                  & ! P0, P1 間の距離
       & q0(1:2),               & ! Q0 の座標
       & q1(1:2),               & ! Q1 の座標
       & q2(1:2),               & ! Q2 の座標
       & dx(1:2)
  ! 2点間の距離のしきい値
  real(8), parameter :: EPS = 2.0d-3
  ! 60 度の回転行列
  ! R60 = ( cos(60)  -sin(60) )
  !       ( sin(60)   cos(60) )
  real(8), parameter ::         &
       & c60 = 0.5d+0,          & ! cos(60)
       & s60 = sqrt(3.0d+0)/2     ! sin(60)
  real(8) :: r60(2, 2) = reshape( (/ c60, s60, -s60, c60 /), (/ 2, 2 /) )

  ! P0, P1 間の距離
  ! dot_product(a(:), b(:)) は配列 a(:), b(:) の内積
  dx(:) = p1(:) - p0(:)
  dist = sqrt(dot_product(dx(:), dx(:)))

  ! 距離がしきい値未満なら始点の座標を表示して終了
  if (dist < EPS) then
     call pprint(p0)
     return
  end if

  ! Q0, Q1, Q2 の座標
  ! 行列とベクトルの積には matmul() を利用する．
  dx(:) = dx(:) / 3             ! [P0, P1] / 3
  q0(:) =                       !******************************
  q2(:) =                       ! この部分を自分で考える
  q1(:) =                       !******************************

  ! 4組の始点と終点 (P0, Q0), (Q0, Q1), (Q1, Q2), (Q2, P1)
  ! に対して再帰的に koch() を呼び出す
  !*****************************************************************
  ! この部分を自分で考える
  !*****************************************************************

  return
end subroutine koch

!------------------------------------------------------------
! 座標値を出力する
!------------------------------------------------------------
subroutine pprint(p)
  implicit none
  real(8), intent(IN) :: p(1:2)

  write(*,'(2E25.16)') p(1:2)

  return
end subroutine pprint

!------------------------------------------------------------
! koch() のためのメインプログラム
!------------------------------------------------------------
program main
  implicit none
  real(8) ::                    &
       & p0(1:2) = (/ 0, 0 /),  & ! 始点 (0, 0)
       & p1(1:2) = (/ 1, 0 /)     ! 終点 (1, 0)

  call koch(p0, p1)
  call pprint(p1)               ! koch() は終点の座標を出力しないため

  stop
end program main

プログラムを実行するとコッホ曲線の頂点の座標が各行に1つ、x 座標と y 座標の組で出力される。これを Gnuplot で描画するには次のようにすればよい。

% ./a.out > koch.dat
% gnuplot
gnuplot> set size ratio 0.3
gnuplot> plot 'koch.dat' with line title 'Koch curve'

コッホ雪片

コッホ曲線を3つつなぎ合わせたものがコッホ雪片 (Koch snowflake) である。コッホ雪片の面積は有限であるが、無限に長い周囲を持つ。

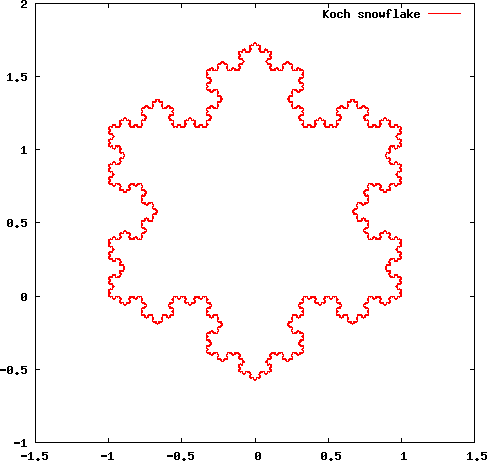図3: コッホ雪片

コッホ曲線

目次

リンク