基礎プロI 100本ノック グラフィクス編
各プログラムにおいて、特に指定が無い限りは入力値が指定された形式であるかどうかをチェックする必要はない(例えば整数型の値を入力させるところでアルファベットを入力された場合など)。
グラフィクス編のプログラムはHandyGraphicを使うこと(プログラミングの練習目的ではEGGX等の他のグラフィクスライブラリでも構わない)。
HandyGraphicのインストール方法はこちらのページの通り。公式ページはこちら。
座標や大きさの単位はピクセルである。特に指定が無い場合は線や塗りつぶし色は初期設定のまま(線は黒、塗りつぶし色は白)でよい。また、プログラムがすぐに終了してしまわないようにHgGetChar関数を使って入力待ち状態を作るとよい。
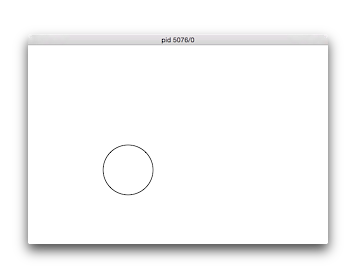
No. 60 円
中心座標を入力させ、横600縦400のウィンドウを開き、入力した座標に半径50の円を描くプログラムを作成せよ。
【実行例、下線部は入力例、実行結果は図の通り】 $ ./knock60 円の中心座標を入力: 200 150 $
実行例のように、2つの値を一度に入力させるために次のように書く方法がある。最初の書式指定文字列中のそれぞれの%dに、そのあとに来る&をつけた変数(変数へのポインタ)が順に対応する。
scanf("%d %d", &cx, &cy);
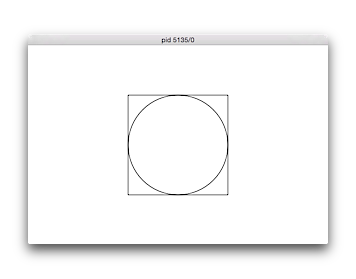
No. 61 正方形と内接円
横600縦400のウィンドウを開き、左下の座標が(200, 100)で大きさが200の正方形と、それに内接する円を描くプログラムを作成せよ。必要な座標はプログラム中でコンピュータに計算させること。
【実行例、実行結果は図の通り】 $ ./knock61 $
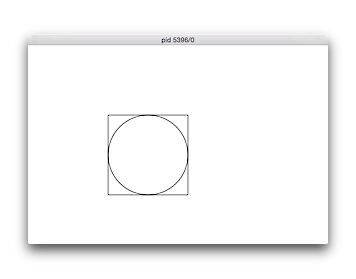
No. 62 円と外接正方形
円の中心座標を入力させ、横600縦400のウィンドウを開き、入力した中心座標に半径80の円と、それに外接する正方形を描くプログラムを作成せよ。
【実行例、下線部は入力例、実行結果は図の通り】 $ ./knock62 円の中心座標を入力: 240 180 $
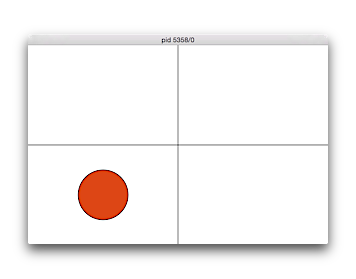
No. 63 象限
中心座標を入力させ、横600縦400のウィンドウを開き、入力した中心座標がウィンドウの左下なら赤、左上なら緑、右下なら青、右上なら黄の塗りつぶし色で、入力した座標に半径50の円を描くプログラムを作成せよ。境界上の場合はどちらの色でも構わない。
【実行例、下線部は入力例、実行結果は図の通り。実行結果では分かりやすいようにウィンドウを4つに区切る線を描いている。】 $ ./knock63 円の中心座標を入力: 150 100 $ ./knock63 円の中心座標を入力: 430 270 $
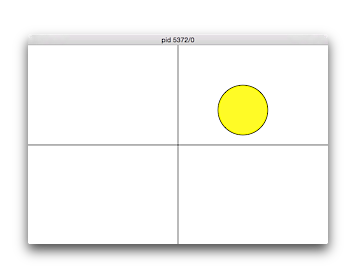
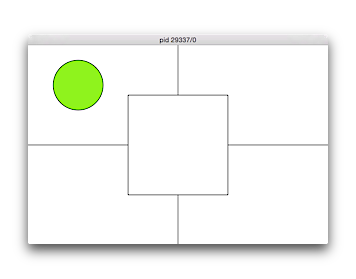
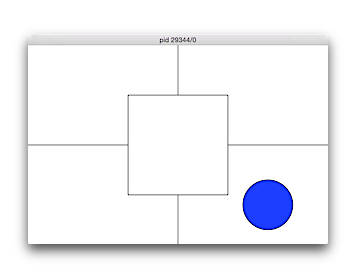
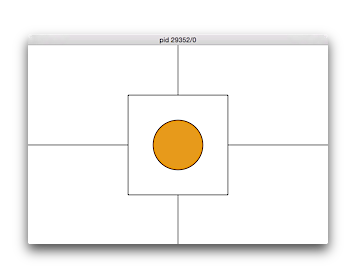
No. 64 象限+中央
中心座標を入力させ、横600縦400のウィンドウを開き、入力した中心座標がウィンドウの中心から左右上下に100以内ならオレンジ、それ以外で、左下なら赤、左上なら緑、右下なら青、右上なら黄の塗りつぶし色で、入力した座標に半径50の円を描くプログラムを作成せよ。境界上の場合はどちらの色でも構わない。
【実行例、下線部は入力例、実行結果は図の通り。実行結果では分かりやすいように各領域を描いている。】 $ ./knock64 円の中心座標を入力: 100 320 $ ./knock64 円の中心座標を入力: 480 80 $ ./knock64 円の中心座標を入力: 480 80 $
No. 65 十字型
中心座標を入力させ、横600縦400のウィンドウを開き、半径10の円を中心座標とその上下左右に5つずつ、中心の間隔を30として描くプログラムを繰り返しを使って作成せよ(具体的な位置関係は下の実行結果例を見よ)。
【実行例、下線部は入力例、実行結果は図の通り。】 $ ./knock65 円の中心座標を入力: 340 180 $

注:同じ位置に2つ円を重ねて描くと他の円に比べて色が濃くなるが(実行例を参照)本課題では気にしなくてもよい。重ねて描かない方法でプログラミングしてもよい。
No. 66 ×型
中心座標を入力させ、横600縦400のウィンドウを開き、半径10の円を中心座標とその斜め方向に5つずつ、中心の間隔を縦方向および横方向それぞれ30(中心の距離が30ではない)として描くプログラムを繰り返しを使って作成せよ(具体的な位置関係は下の実行結果例を見よ)。
【実行例、下線部は入力例、実行結果は図の通り。】 $ ./knock66 円の中心座標を入力: 340 180 $
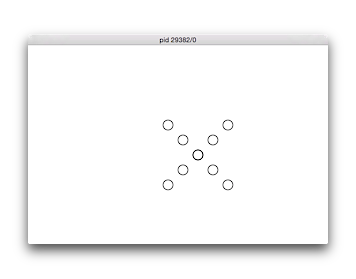
注:同じ位置に2つ円を重ねて描くと他の円に比べて色が濃くなるが(実行例を参照)本課題では気にしなくてもよい。重ねて描かない方法でプログラミングしてもよい。
No. 67 5×5
中心座標を入力させ、横600縦400のウィンドウを開き、半径10の円を中心座標とその上下左右に5行五列の25個、中心の間隔を縦方向および横方向それぞれ30として描くプログラムを繰り返しを使って作成せよ(具体的な位置関係は下の実行結果例を見よ)。
【実行例、下線部は入力例、実行結果は図の通り。】 $ ./knock66 円の中心座標を入力: 340 180 $
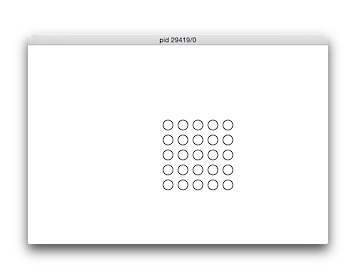
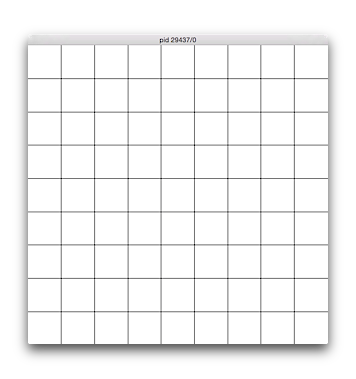
No. 68 マス目
マス目の数(1以上の整数値)を入力させ、横600縦600のウィンドウを開き、ウィンドウの縦横がマス目の数に区切られるよう等間隔に線を描くプログラムを作成せよ。整数値の計算の場合、入力値によっては多少の誤差が生じるが、できるだけ誤差が小さくなるよう工夫せよ。
【実行例、下線部は入力例、実行結果は図の通り。】 $ ./knock68 マス目の数: 9 $
No. 69 市松模様
マス目の数(1以上の整数値)を入力させ、横600縦600のウィンドウを開き、ウィンドウの縦横がマス目の数に区切られ、マス目を白と黒で交互に塗りつぶして描くプログラムを作成せよ(白と黒が交互になっていればよい)。整数値の計算の場合、入力値によっては多少の誤差が生じるが、できるだけ誤差が小さくなるよう工夫せよ。
【実行例、下線部は入力例、実行結果は図の通り。】 $ ./knock69 マス目の数: 9 $

ヒント:最低限、黒いマス目だけ描いていけばよい(罫線を描かなくてもよい)。白と黒の塗り潰し四角を描いていくという方法もある。
No. 70 bound
横600縦400のウィンドウ内を、半径30の円が、中心の初期位置(0,0)、初速(5,3)で移動し、ウィンドウの端に円の中心が達したら反対方向に跳ね返る動きをするプログラムを作成せよ。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock70 $
No. 71 bound改
横600縦400のウィンドウ内を、半径30の円が、中心の初期位置(30,30)、初速(5,3)で移動し、ウィンドウの端に円の端が接したら反対方向に跳ね返る動きをするプログラムを作成せよ。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock71 $
円の半径の分だけウィンドウが狭いと考えればよい。
No. 72 ワープ
横600縦400のウィンドウ内を、半径30の円が、中心の初期位置(30,30)、初速(5,3)で移動し、ウィンドウの端に円の中心が接したら反対側の端から出現する(左右、上下の端が繋がっているようになっている)プログラムを作成せよ。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock72 $
No. 73 bound×2
横600縦400のウィンドウ内を、半径30の円が2つ、中心の初期位置(30,30)、それぞれの初速が(5,3)と(3,5)で移動し、ウィンドウの端に円の端が接したら反対方向に跳ね返る動きをするプログラムを作成せよ。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock73 $
No.72の円を2つにする。
No. 74 衝突判定
横600縦400のウィンドウ内を、半径30の円が2つ、そらぞれの中心の初期位置(30,30)と(570,370)、それぞれの初速が(5,3)と(-3,-5)で移動し、ウィンドウの端に円の端が接したら反対方向に跳ね返る動きをし、円が接するか重なる場合は赤、そうでない場合は青で塗りつぶして表示するプログラムを作成せよ。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock74 $
No.73をベースに、重なるか判定して塗りつぶし色を決める。
No. 75 bound×5
横600縦400のウィンドウ内を、半径30の円が5つ、中心の初期位置(30,30)、それぞれの初速が(1,5)、(2,4)、(3,3)、(4,2)、(5,1)で移動し、ウィンドウの端に円の端が接したら反対方向に跳ね返る動きをするプログラムを作成せよ。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock75 $
No.73の円を5つにする。変数を配列化することでプログラムは単純にできる。
No. 76 色が変わるbound×5
横600縦400のウィンドウ内を、半径30の円が5つ、中心の初期位置(30,30)、それぞれの初速が(1,5)、(2,4)、(3,3)、(4,2)、(5,1)で移動し、ウィンドウの端に円の端が接したら反対方向に跳ね返る動きをするプログラムを作成せよ。ただし、それぞれの円の色は、壁に当たるごとに赤→青→緑→黄と変化し、黄の次は赤に戻る。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock76 $
No.76に円の色を設定する処理を追加する。それぞれの円ごとに現在の色を表す値を覚えておく配列を作り、その値を壁が当たるごとに変化させる。そして、描こうとする円に対応する色の値に応じて色を設定する。
No. 77 boundする円とマス目
横400縦400のウィンドウ内を、半径30の赤色の円が、中心の初期位置(30,30)、初速(5,3)で移動し、ウィンドウの端に円の端が接したら反対方向に跳ね返る。ウィンドウは10x10のマス目で区切られており、円の中心が通過したマス目は黒色に塗りつぶされていくプログラムを作成せよ。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock77 $
マス目は、白色か黒色の正方形を10x10描けばよい。各マス目がどちらの色か覚えておく10x10の2次元配列を使う。例えば、配列要素の値が0の時は白(通過していない)、1の時は黒(通過した)、とすると、初期値をすべて0にしておき、円が通過したマス(=円の中心座標が入っているマス目)に対応する配列要素の値を1に書き換えていく。マス目を描く時には、対応する配列要素の値が0の時は白、1の時は黒で描いていく。先にマス目を描いてから円を描くこと。
No. 78 放物線運動
横600縦400のウィンドウを開き、半径30の円が、初期位置(30,30)、x方向の初速10、y方向の初速25で、下向きに重力が働くものとして放物線運動する様子をアニメーション表示するプログラムを作成せよ(重力加速度の値は下記参照)。1画面ごとの休止時間は0.05秒でよい。
【実行例、実行結果は図の通り。】 $ ./knock78 $
t回目の繰り返しの時に、円の中心座標(x,y)は次の式で計算できる。
x = x0 + u * t;
y = y0 + v * t + a * t * t / 2;
uとvはx,y軸方向の初速、aは重力加速度で-1として計算せよ。
No. 79 モンテカルロ法
まず横400縦400のウィンドウを開く。
次に、0から399までの乱数を2つ生成してx,y座標とし、原点(0,0)からの距離が400以下であれば赤、400よりも大きければ青の小さな円をその位置に描く。この手順を繰り返し、正方形中のランダムな位置に円を10000個描きながら赤の点の個数を数えておき、点の個数から円周率の近似値を求めよ。
円周率の近似値は次の式で計算できる。
π=(赤い点の個数 * 4.0)/全部の点の個数
小数点以下の値を扱いたいのでπの計算結果はdouble型で宣言すること(右辺の計算式は4.0と書くことによって自動的にdouble型で計算される)。double型の値をprintf関数で表示するには、%lfを指定する。例えば次のとおり:
double pi; // πの計算結果を格納する変数
// 途中省略
pi = redPoints * 4.0 / totalPoints;
printf("pi = %lf\n", pi);
【実行例、実行結果は図の通り(ただし計算結果の値は実行するたびに異なる)】 $ ./knock79 pi = 3.152000 $
乱数の使い方は演習資料の高度なテクニック集を見よ。0から399の乱数は、rand() % 400 で計算できる(400で割った余りなので399までになることに注意)。なお、図形表示は計算の過程を視覚化しているだけで、本質的な計算とは無関係である。全部描いてから赤の点の個数を数えることはできないので、赤の点を表示する度に回数を数えておくようにせよ。
このような乱数を使ったシミュレーション手法をモンテカルロ法と呼ぶ。例えば囲碁のAIに使用されて格段に強くなった実績がある。試行回数(サンプル数)が多くなるほど理論値に収束することが期待できるが、試行回数が少ないと誤差は大きくなる。10000個ではあまり正確な値にならない。個数を変えて試してみるとよい。