プログラム断片(2008/06/15)
for VisualWorks 7.6 with Jun780, Prologインタプリタのマニュアル(PDF), Lispインタプリタのマニュアル(PDF)
#include <stdio.h>
#include <stdlib.h>
int sigma(int n)
{
int result, number;
if (n < 0)
{
fprintf(stderr, "error: can't compute sigma(%d)\n", n);
exit(EXIT_FAILURE);
}
result = 0;
for (number = 1; number <= n; number++)
{
result = result + number;
}
return(result);
}
int main(void)
{
int n;
for (n = 10; n >= 0; n--)
{
printf("sigma(%d) = %d\n", n, sigma(n));
}
return(EXIT_SUCCESS);
}
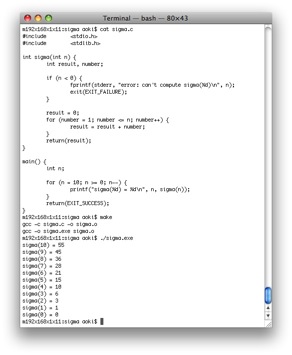 |
sigma(10) = 55
sigma(9) = 45
sigma(8) = 36
sigma(7) = 28
sigma(6) = 21
sigma(5) = 15
sigma(4) = 10
sigma(3) = 6
sigma(2) = 3
sigma(1) = 1
sigma(0) = 0
|
|
| sigma |
sigma :=
[:n |
n < 0 ifTrue: [self error: 'can not compute sigma(' , n printString , ')'].
n = 0 ifTrue: [0] ifFalse: [n + (sigma value: n - 1)]].
Transcript clear.
(36 to: 0 by: -1) do:
[:n |
Transcript
nextPutAll: 'sigma(';
nextPutAll: n printString;
nextPutAll: ') = ';
nextPutAll: (sigma value: n) printString;
cr;
flush]
?- remove.
sigma(0,0).
sigma(N,F) :-
integer(N),
>(N,0),
-(N,1,M),
sigma(M,R),
+(N,R,F).
sigmas(N) :-
integer(N),
>=(N,0),
sigma(N,X),
write("sigma("),
write(N),
write(") = "),
write(X),
nl,
-(N,1,M),
sigmas(M).
sigmas(~).
?- clear,
sigmas(36).
(defun sigma (n)
(cond ((not (integerp n)) nil)
((< n 0) nil)
((= n 0) 0)
(t (+ n (sigma (- n 1))))))
(defun sigmas (n)
(cond ((not (integerp n)) nil)
((< n 0))
(t (progn
(princ "sigma(")
(princ n)
(princ ") = ")
(print (sigma n))
(sigmas (- n 1))))))
(progn
(clear)
(sigmas 36))
#include <stdio.h>
#include <stdlib.h>
int factorial(int n)
{
int result, number;
if (n < 0)
{
fprintf(stderr, "error: can't compute factorial(%d)\n", n);
exit(EXIT_FAILURE);
}
result = 1;
for (number = 1; number <= n; number++)
{
result = result * number;
}
return(result);
}
int main(void)
{
int n;
for (n = 10; n >= 0; n--)
{
printf("%d! = %d\n", n, factorial(n));
}
return(EXIT_SUCCESS);
}
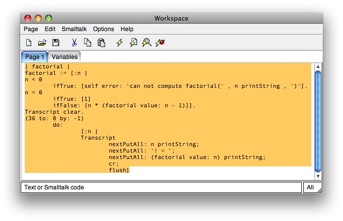
| factorial |
factorial :=
[:n |
n < 0 ifTrue: [self error: 'can not compute factorial(' , n printString , ')'].
n = 0 ifTrue: [1] ifFalse: [n * (factorial value: n - 1)]].
Transcript clear.
(36 to: 0 by: -1) do:
[:n |
Transcript
nextPutAll: n printString;
nextPutAll: '! = ';
nextPutAll: (factorial value: n) printString;
cr;
flush]
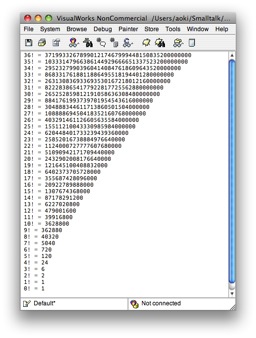 |
36! = 371993326789901217467999448150835200000000
35! = 10333147966386144929666651337523200000000
34! = 295232799039604140847618609643520000000
33! = 8683317618811886495518194401280000000
32! = 263130836933693530167218012160000000
31! = 8222838654177922817725562880000000
30! = 265252859812191058636308480000000
29! = 8841761993739701954543616000000
28! = 304888344611713860501504000000
27! = 10888869450418352160768000000
26! = 403291461126605635584000000
25! = 15511210043330985984000000
24! = 620448401733239439360000
23! = 25852016738884976640000
22! = 1124000727777607680000
21! = 51090942171709440000
20! = 2432902008176640000
19! = 121645100408832000
18! = 6402373705728000
17! = 355687428096000
16! = 20922789888000
15! = 1307674368000
14! = 87178291200
13! = 6227020800
12! = 479001600
11! = 39916800
10! = 3628800
9! = 362880
8! = 40320
7! = 5040
6! = 720
5! = 120
4! = 24
3! = 6
2! = 2
1! = 1
0! = 1
|
|
?- remove.
factorial(0,1).
factorial(N,F) :-
integer(N),
>(N,0),
-(N,1,M),
factorial(M,R),
*(N,R,F).
factorials(N) :-
integer(N),
>=(N,0),
factorial(N,X),
write(N),
write("! = "),
write(X),
nl,
-(N,1,M),
factorials(M).
factorials(~).
?- clear,
factorials(36).
(defun factorial (n)
(cond ((not (integerp n)) nil)
((< n 0) nil)
((= n 0) 1)
(t (* n (factorial (- n 1))))))
(defun factorials (n)
(cond ((not (integerp n)) nil)
((< n 0))
(t (progn
(princ n)
(princ "! = ")
(print (factorial n))
(factorials (- n 1))))))
(progn
(clear)
(factorials 36))
#include <stdio.h>
#include <stdlib.h>
int fibonacci(int n)
{
int result, number;
if (n < 0)
{
fprintf(stderr, "error: can't compute fibonacci(%d)\n", n);
exit(EXIT_FAILURE);
}
if (n == 0)
{
result = 0;
}
else if (n == 1)
{
result = 1;
}
else
{
result = fibonacci(n - 1) + fibonacci(n - 2);
}
return(result);
}
int main(void)
{
int n;
for (n = 20; n >= 0; n--)
{
printf("fibonacci(%d) = %d\n", n, fibonacci(n));
}
return(EXIT_SUCCESS);
}
| fibonacci |
fibonacci :=
[:n |
n < 0 ifTrue: [self error: 'can not compute fibonacci(' , n printString , ')'].
n = 0
ifTrue: [0]
ifFalse:
[n = 1
ifTrue: [1]
ifFalse: [(fibonacci value: n - 1) + (fibonacci value: n - 2)]]].
Transcript clear.
(20 to: 0 by: -1) do:
[:n |
Transcript
nextPutAll: 'fibonacci(';
nextPutAll: n printString;
nextPutAll: ') = ';
nextPutAll: (fibonacci value: n) printString;
cr;
flush]
参考:Smalltalk版;リフレクションによる連想計算でフィボナッチ数を計算
?- remove.
fibonacci(0,0).
fibonacci(1,1).
fibonacci(N,F) :-
integer(N),
>(N,1),
-(N,1,N1),
-(N,2,N2),
fibonacci(N1,A1),
fibonacci(N2,A2),
+(A1,A2,F).
fibonaccies(N) :-
integer(N),
>=(N,0),
fibonacci(N,X),
write("fibonacci("),
write(N),
write(") = "),
write(X),
nl,
-(N,1,M),
fibonaccies(M).
fibonaccies(~).
?- clear,
fibonaccies(20).
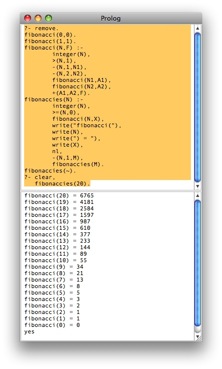 |
fibonacci(20) = 6765
fibonacci(19) = 4181
fibonacci(18) = 2584
fibonacci(17) = 1597
fibonacci(16) = 987
fibonacci(15) = 610
fibonacci(14) = 377
fibonacci(13) = 233
fibonacci(12) = 144
fibonacci(11) = 89
fibonacci(10) = 55
fibonacci(9) = 34
fibonacci(8) = 21
fibonacci(7) = 13
fibonacci(6) = 8
fibonacci(5) = 5
fibonacci(4) = 3
fibonacci(3) = 2
fibonacci(2) = 1
fibonacci(1) = 1
fibonacci(0) = 0
|
|
参考:Prolog版;リフレクションによる連想計算でフィボナッチ数を計算
(defun fibonacci (n)
(cond ((not (integerp n)) nil)
((< n 0) nil)
((= n 0) 0)
((= n 1) 1)
(t (+ (fibonacci (- n 1))
(fibonacci (- n 2))))))
(defun fibonaccis (n)
(cond ((not (integerp n)) nil)
((< n 0))
(t (progn
(princ "fibonacci(")
(princ n)
(princ ") = ")
(print (fibonacci n))
(fibonaccis (- n 1))))))
(progn
(clear)
(fibonaccis 20))
参考:Lisp版;リフレクションによる連想計算でフィボナッチ数を計算
#include <stdio.h>
#include <stdlib.h>
int ackermann(int m, int n)
{
int result, number;
if (m < 0)
{
fprintf(stderr, "error: can not compute ackermann(%d,%d)\n", m, n);
exit(EXIT_FAILURE);
}
if (n < 0)
{
fprintf(stderr, "error: can not compute ackermann(%d,%d)\n", m, n);
exit(EXIT_FAILURE);
}
if (m == 0)
{
result = n + 1;
}
else if (n == 0)
{
result = ackermann((m - 1), 1);
}
else
{
result = ackermann((m - 1), ackermann(m, (n - 1)));
}
return(result);
}
int main(void)
{
int m, n;
for (m = 3; m >= 0; m--)
{
for (n = 4; n >= 0; n--)
{
printf("ackermann(%d,%d) = %d\n", m, n, ackermann(m, n));
}
}
return(EXIT_SUCCESS);
}
| ackermann |
ackermann :=
[:m :n |
m < 0 ifTrue: [self error: 'can not compute ackermann(' , m printString , ',' , n printString , ')'].
n < 0 ifTrue: [self error: 'can not compute ackermann(' , m printString , ',' , n printString , ')'].
m = 0
ifTrue: [n + 1]
ifFalse:
[n = 0
ifTrue: [ackermann value: m - 1 value: 1]
ifFalse: [ackermann value: m - 1 value: (ackermann value: m value: n - 1)]]].
Transcript clear.
(3 to: 0 by: -1) do:
[:m |
(4 to: 0 by: -1) do:
[:n |
Transcript
nextPutAll: 'ackermann(';
nextPutAll: m printString;
nextPutAll: ',';
nextPutAll: n printString;
nextPutAll: ') = ';
nextPutAll: (ackermann value: m value: n) printString;
cr;
flush]]
?- remove.
ackermann(0,N,A) :-
+(N,1,A).
ackermann(M,0,A) :-
-(M,1,M1),
ackermann(M1,1,A).
ackermann(M,N,A) :-
integer(M),
integer(N),
>(M,0),
>(N,0),
-(M,1,M1),
-(N,1,N1),
ackermann(M,N1,A1),
ackermann(M1,A1,A).
ackermanns(M,N) :-
integer(N),
>=(N,0),
ackermann(M,N,A),
write("ackermann("),
write(M),
write(","),
write(N),
write(") = "),
write(A),
nl,
-(N,1,N1),
ackermanns(M,N1).
ackermanns(~,~).
?- clear,
ackermanns(3,4),
ackermanns(2,4),
ackermanns(1,4),
ackermanns(0,4).
(defun ackermann (m n)
(cond ((not (integerp m)) nil)
((not (integerp n)) nil)
((< m 0) nil)
((< n 0) nil)
((= m 0) (+ n 1))
((= n 0) (ackermann (- m 1) 1))
(t (ackermann (- m 1) (ackermann m (- n 1))))))
(defun ackermanns (m n)
(cond ((not (integerp n)) nil)
((< n 0) nil)
(t (progn
(princ "ackermann(")
(princ m)
(princ ",")
(princ n)
(princ ") = ")
(print (ackermann m n))
(ackermanns m (- n 1))))))
(progn
(clear)
(ackermanns 3 4)
(ackermanns 2 4)
(ackermanns 1 4)
(ackermanns 0 4))
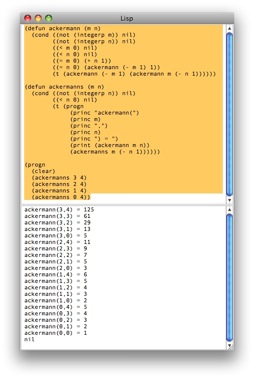 |
ackermann(3,4) = 125
ackermann(3,3) = 61
ackermann(3,2) = 29
ackermann(3,1) = 13
ackermann(3,0) = 5
ackermann(2,4) = 11
ackermann(2,3) = 9
ackermann(2,2) = 7
ackermann(2,1) = 5
ackermann(2,0) = 3
ackermann(1,4) = 6
ackermann(1,3) = 5
ackermann(1,2) = 4
ackermann(1,1) = 3
ackermann(1,0) = 2
ackermann(0,4) = 5
ackermann(0,3) = 4
ackermann(0,2) = 3
ackermann(0,1) = 2
ackermann(0,0) = 1
|
|
for VisualWorks 7.6 with Jun780, Prologインタプリタのマニュアル(PDF), Lispインタプリタのマニュアル(PDF)
Updated: 2015/11/08 (Created: 2008/06/15)


