C言語で扱える実数値は,2進数の有限小数で表された数値である.例えば次のようなものである.
1.5(10) = 1.1(2)
3.25(10) = 11.01(2)
理論的には小数が無限に続く値でも,そのうちの有限個の桁数でその値を表すしかない.
例えば,0.1 を2進数の小数で表すと
0.1(10) = 0.000110011001100110011...(2)
と無限に続くが,コンピュータの内部では有限桁で丸められている.
このような場合には,本当の値ではなく,近似値でしか表すことができない.
科学計算では非常に大きな実数値や非常に小さな実数値も扱うことがある.
そのようなときには,通常の10進数の表記ではなくて,次のような指数表記で表すれば
無駄な 000...000 という桁を表記しなくてもよくなる.
12345678900000000000000000000 = 1.23456789 * 1028
0.00000000000000000000123456789 = 1.23456789 * 10-21
これは,2進数表現でも同じで,
110110100100000000000000000000000 = 1.101101001 * 232
0.00000000000000000000000001101101001 = 1.101101001 * 2-26
と指数表記することができる.
このような指数表記の, 1.101101001 という値を仮数,32 および -26 という値を指数と呼ぶ.
仮数と指数と(さらに+−の符号と)を用いて表された実数値のことを浮動小数点数と呼ぶ.
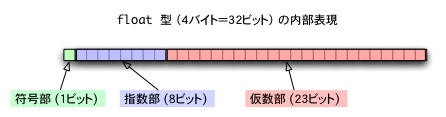
float型は4バイト=32ビットのサイズを持ち,そのビットを次のように,符号,指数,仮数を表すために用いる.

指数部-127 が指数の値となる.仮数部は仮数の小数点以下を表している.すなわち,仮数は仮数部の先頭に 1. を付加したものになる.
float の表す値 = (-1)符号部 × 2指数部-127 × 1.仮数部
float 型の精度(有効桁数)は2進数にして 24 (=23+1) 桁であり,10進数では約 7 桁となる.
指数部も有限であるため, float で表すことのできる実数の絶対値は次のような範囲に限られる.
1.175494 10-38 < float の絶対値 < 3.402823 10+38
この下限値と上限値とは,ヘッダファイル float.h で FLT_MIN および FLT_MAX という名前でマクロ定義されている.
#include <stdio.h> #include <float.h> int main() { printf("FLT_MIN = %e, FLT_MAX =%e\n", FLT_MIN, FLT_MAX); return 0; }
FLT_MIN = 1.175494e-38, FLT_MAX = 3.402823e+38
float 型に比べて,約倍の精度をもった浮動小数点型の型が double である. double 型は 8バイト=64ビットのサイズであり,その内部表現は次のようになる.

指数部-1023 が指数の値となる.仮数部は仮数の小数点以下を表している.すなわち,仮数は仮数部の先頭に 1. を付加したものになる.
double の表す値 = (-1)符号部 × 2指数部-1023 × 1.仮数部
double 型の精度(有効桁数)は2進数にして 53 (=52+1) 桁であり,10進数では約 15 桁となる.
指数部も有限であるため, double で表すことのできる実数の絶対値は次のような範囲に限られる.
2.225074 10-308 < double の絶対値 < 1.797693 10+308
この下限値と上限値とは,ヘッダファイル float.h で DBL_MIN および DBL_MAX という名前でマクロ定義されている.
#include <stdio.h> #include <float.h> int main() { printf("DBL_MIN = %e, DBL_MAX =%e\n", DBL_MIN, DBL_MAX); return 0; }
DBL_MIN = 2.225074e-308, DBL_MAX = 1.797693e+308
現在のコンピュータでは, float 型よりも double 型を使うことが多い.その理由は
1. 精度が良い.
2. 計算速度が速い.
ということがある.速度が速い理由は,現在のほとんどのコンピュータには double 型のデータを専門に扱う回路が付いているからである.
float 型の計算を行うときには,一度 double 型に変換した後,この回路で計算し,
その後再び float 型に変換される.したがって, float 型の方が計算時間が多くかかることになる.
float 型にはメモリサイズが double 型の半分という利点があるが,
現在のコンピュータは十分なメモリを持っているので,その利点が有効であることはあまりない.
数値を表す型には, char, int, flat, double など数種類の型があるが, それらの値を互いに他の型に変換することを型変換という.
同じ型同士の四則演算の結果は,その同じ型である.たとえば, float 型 + float 型の結果は float 型であり, int型 / int型 の結果は int 型である.
そう! 整数型同士の割り算 1/3 の結果は整数型だから,
0.333333 ではなくて, 0 である.
これについては,後でもう一度述べる.
しかし,異なる型の四則演算(これを混合演算という)は,
精度の低い方が高い方へ自動的に型変換されたのちに演算される.
ここで,精度が低い高いは次の約束に従う.(不等号の意味は 精度が低い < 精度が高い)
char < int < long int < float < double < long double
例えば, int型 + double型 は int型を double 型に型変換したのちに演算される. (その結果は double 型となる)
char a, b;
int i, j;
float s, t;
doubler x, y;
i + j; /* int型 */
s * t; /* float型 */
i * x; /* double型 */
a * s + t / x; /* a * f はfloat型, t / x はdouble型, a * s + t / x はdouble型 */
i / j * s / x; /* i / j はint型, i / j * s はfloat型, i / j * s / x はdouble型 */
以上のように,数値の四則演算については型が混じっていても,適当にうまく計算できるようになっている.しかし,間違いやすいので注意すべきことが一つある.それは int型 / int型 の結果も int型 であるということだ. 実際の値は,割り算の商(除算の整数部分)となる. したがって, 1/3 の結果は浮動小数点数の 0.333333 ではなくて, 整数の 0 である.
値を変数に代入しようとしたとき, 値の型と変数の型とが異なるときには, 代入先の変数の型に自動的に変換される.
整数型の値を浮動小数点型の変数に代入すると,小数点以下が .000000 となる.
浮動小数点型の値を整数型の変数に代入すると,小数点以下が切り捨てられる.
main()
{
int i;
double x;
i = 12;
x = i; /* int型をdouble型に変換 */
printf("%f\n", x);
x = 12.345;
i = x; /* double型をint型に変換 */
printf("%d\n", i);
x = -12.345;
i = x; /* double型をint型に変換 */
printf("%d\n", i);
}
12.000000 12 -12
関数の引数へ値を渡すときに, 値の型と関数宣言の際に定義された引数の型とが異なるときには, 引数の型に自動的に変換される.
void f(double x)
{
printf("%f\n", x);
}
void g(int x)
{
printf("%d\n", x);
}
main()
{
int i = 10;
double z = 12.345;
f(i); /* int 型の実引数が double 型に変換された後,仮引数に渡される */
g(z); /* double 型の実引数が int 型に変換された後,仮引数に渡される */
}
10.000000 12
上記のような暗黙の型変換の他に,キャストを用いて明示的に型変換を行うこともできる.
キャストとは (double) のように型名を括弧でくくったものであり, (double)a のように,型変換を行いたい変数や式や値の前に付ける.
char a, b;
int i, j;
float s, t;
doubler x, y;
(double) a ; /* double型 */
(float) (i + j); /* float型 */
(char) x; /* char型 */
(int) (i * x); /* int型 */
先ほど注意した通り, int型 / int型の結果は int型であり,その値は除算の整数部分となる. 普通の除算(小数点以下も含めた値)の値が欲しいときには,浮動小数点型に明示的に型変換する 必要がある.
main()
{
int i, j;
double x;
i = 1;
j = 3;
x = i / j; /* i / j の結果は整数型である. */
printf("%f\n", x); /* その結果は 0.000000 */
x = (double)i / (double)j; /* i と j をdouble型に明示的に型変換している */
printf("%f\n", x); /* これで期待通りの結果 0.333333 となる. */
x = (double) (i / j); /* これは i / j の結果 0 をdouble型に変換するだけである */
printf("%f\n", x); /* 結果は 0.000000 となる.これでは期待はずれ. */
}
(double)i + (double)j の二つのキャストのうち,一方だけでも同様の結果が得られる. (混合演算による暗黙の型変換がなされるため)
0.000000 0.333333 0.000000
浮動小数点値の小数点以下を切り捨てて整数部分だけを取り出したいときには, (int) でキャストするとよい.
main()
{
double x = 3.99, y = 2.99;
int i;
i = (int)x + (int)y; /* x の整数部分と y の整数部分とを加える */
printf("%d\n", i);
}
5
次のプログラムは 2/3 + 3/5 + 5/2 = 3.766667 を計算するためのものであるが, 実際の結果は 2.000000 となってしまう.キャストを用いて型変換をすることにより, 正確な答えが出るようにせよ.
main()
{
int i = 2, j = 3, k = 5;
double x;
x = i / j + j / k + k / i; /* この式の右辺中に,キャストをいくつか入れる */
printf("%f\n", x);
}
ここで説明したことのいくつかは正確ではない.些細なことであるが,それを説明しておく.
char 型は常に int 型に変換されてから演算される.従って char型+char型 という演算結果は, int型である.その証拠を sizeof を使って見てみよう. char型なら1バイト, int型なら4バイトである.
main()
{
char a, b;
printf("%d\n", sizeof(a+b)); /* a+b という演算結果のメモリサイズを表示 */
}
4
int 型よりも float 型の方が精度が高いというのはある意味で嘘である. int型は(整数部分だけに限ると)10桁ほどの精度があるが, float型は7桁ほどしかない.
main()
{
int i = 123456789;
float f;
f = i;
printf("%d %f\n", i, f);
}
123456789 123456792.000000
実数を浮動小数点数すなわち有限桁数の2進数によって計算すると,どうしても誤差が生じる. それを丸め誤差という.
たとえば,float 型で表した実数は,その有効数字は約 7 桁であり, それ以上の精度を求めることはできない.
さらに, float 型で表した実数が常に有効数字 6 桁を持っているかというと,そうとは限らない. 始めには 6 桁の有効桁数を持っていた数値が,計算を繰り返すことにより精度が劣化することがある. その場合を見てみよう.
値が近い二つの数を引き算することにより,その有効桁数が落ちる.これを桁落ちという. 例えば次の計算では, 6 桁の有効桁数を持った2数の引き算の結果の有効桁数が 2 桁となっている.
123.456 - 123.444 = 0.012
桁落ちが生じる例として,2次方程式 a x2 + b x + c == 0 で |ac| << |b|2 あるもの( << は比較してかなり差があるという意味)の解を, 解の公式 α = (- b + √d )/(2a) , β = (- b - √d)/(2a) で求める計算を見てみよう (ここで d = b2-4ac である).
具体的な例として x2 - 333.33 x + 1.23456 == 0 の解を求めてみる(真の解は 333.329296… と 0.00370372485… である).
#include <stdio.h>
#include <math.h>
int main()
{
float a, b, c, sd, alpha, beta, z;
a = 1.00000;
b = -333.333;
c = 1.23456;
sd = sqrt( b*b - 4*a*c );
alpha = (-b + sd) / (2*a);
beta = (-b - sd) / (2*a);
printf("alpha = %15e beta = %15e\n", alpha, beta);
printf(" %15e %15e\n", 333.329296, 0.00370372485);
printf("( sd= %f )\n", sd);
return 0;
}
数学関数 sqrt を使っているので,コンパイル時には数学関数ライブラリをリンクするオプション -lm を付ける必要がある.
gcc filename.c -lm
その結果は次のようになる.上段が解の公式で求めた解.その下が真の解である.
alpha = 3.333293e+02 beta = 3.707886e-03
3.333293e+02 3.703725e-03
( sd= 333.325592 )
alpha はほぼ正しい値となっているが,beta はかなりの誤差があり,有効桁数は3桁ほどである.
その原因は,beta を求めるときの -b - sd という計算にある.-b = 333.333 と sd = 333.325 との差は 0.008 となり,桁落ちをおこしている.
桁落ちを回避するためには,計算手順を考え直して, 大きさの近い2数の引き算を避けるようにするしかない. 上の問題の場合には,alpha * beta = c / a という解と係数の関係を用いて, beta = c / (a * alpha) という式から beta を計算すると,桁落ちを起こす引き算を回避できる.
#include <stdio.h>
#include <math.h>
int main()
{
float a, b, c, sd, alpha, beta, z;
a = 1.00000;
b = -333.333;
c = 1.23456;
sd = sqrt( b*b - 4*a*c );
alpha = (-b + sd) / (2*a);
beta = c/(a*x);
printf("alpha = %15e beta = %15e\n", alpha, beta);
printf(" %15e %15e\n", 333.329296, 0.00370372485);
printf("( sd= %f )\n", sd);
return 0;
}
alpha = 3.333293e+02 beta = 3.703725e-03
3.333293e+02 3.703725e-03
絶対値が大きな値と小さな値とを加えた場合,小さい方の数値がもつ情報が失われる. たとえば, float 型の精度は約6桁であるから,float 型の数値 77777.7 と 1.23456 とを加えると, 結果も6桁であるから, 77778.9 となる.すなわち, 1.23456 がもつ情報のうちの下4桁の情報が失われている.
77777.7 + 1.23456 = 77778.9
多数のデータを足し合わせるときには,この情報落ちが累積して無視できなくなる.
次のプログラムは, f(x) = √(1-x^2) を区間 [0, 1] で積分した値の 4倍が円周率πであることを用いて, 区間 [0, 1] を 1000000 等分した点での f(x) の値を加えて 1000000 で割り 4 倍することで 円周率 3.14159265... を求めるものである.
#include <stdio.h>
#define N 1000000
#define sqr(x) ((x)*(x))
int main()
{
float f[N];
int i;
float s;
for (i = 0; i < N; i++) {
f[i] = sqrt( 1 - sqr((i+0.5) / N));
}
s = 0.0;
for (i = 0; i < N; i++) {
s += f[i];
}
printf("%f\n", 4.0 * s / N);
return 0;
}
数学関数 sqrt を用いているので,コンパイル時にリンクオプション -lm を付ける必要がある.
gcc filename.c -lm
しかし,実行結果は次の通りで,その有効桁数は4桁ほどしかない. これは,ループの後半において,値を繰り返し加えて蓄積した s の値が f[i] の値と比較して非常に大きくなったため, s += f[i] の加算において情報落ちが発生し,それが累積したためである. (情報落ちという言葉に惑わされて,本当の値よりも小さくなってしまうと思いがちだが,この場合のように,そうとは限らない.)
3.141616
このような情報落ちも,計算手順の工夫により回避することができる.
次のプログラムでは,加えるべき値と実際に加わった値との差(積み残し)を 考慮することで情報落ちを防いでいる.
#include <stdio.h>
#define N 1000000
#define sqr(x) ((x)*(x))
int main()
{
float f[N];
int i;
float r, s, t;
for (i = 0; i < N; i++) {
f[i] = sqrt( 1 - sqr((i+0.5) / N));
}
r = s = 0; /* r は積み残し, s は総和 */
for (i = 0; i < N; i++) {
t = s + (f[i] + r); /* 前回までの総和に f[i] と前回までの積み残しとを加えたものが,今回の結果 */
r = (f[i] + r) - (t - s); /* 加えるべき値 (f[i] + r) と実際に加わった値 (t - s) との差が,今回の積み残し */
s = t;
}
printf("%f\n", 4.0 * s / N);
return 0;
}
3.141593
100001.0, 0.123456, 0.111111, -100000.0 という4個の数値の和は 1.234567 であるが, 次のプログラムで計算すると,違う値となる.
#include <stdio.h>
main()
{
float a, b, c, d, s;
a = 100001.0;
b = 0.123456;
c = 0.111111;
d = -100000.0;
s = 0.0;
s += a;
s += b;
s += c;
s += d;
printf("%f\n", s);
}
1.234375
値が違う理由は,情報落ちが起こっているせいである.値を加える順序を変更して,より正確な値が出るようにプログラムを変更せよ.
コンパイル時に -lm オプションを付けることで,標準Cライブラリにあるいくつかの算術関数を使うことができる.
使用に先立ってプログラム中に次のインクルード命令を書く必要がある.
#include <math.h>
算術関数を使用したときには,コンパイル時に -lm オプションを付ける.
gcc filename.c -lm
次に挙げる関数はよく使う関数であるが,授業では解説しない. どのような関数があったかを憶えておくだけで良い.
double ceil(double x) x 以上の最小の整数 double floor(double x) x 以下の最大の整数
double fabs(double x) x の絶対値
double fmod(double x, double y) x を y で割った余り
double pow(double x, double y) xy double sqrt(double x) √x
double exp(double x) ex double log(double x) log x
double sin(double x) sin x (x の単位はラジアン) double cos(double x) cos x (x の単位はラジアン) double tan(double x) tan x (x の単位はラジアン)
double asin(double x) arcsin x double acos(double x) arccos x double atan(double x) arctan x double atan2(double x, double y) arctan y/x
この他にもあるが省略する.