バックトラック法 (backtracking)あるいは後戻り法とは,問題の解を見つけるために, 解の候補をすべて調べることを組織的にかつ効率よく行うための技法である。 難しい組み合わせ的な問題を解くための技法であり,応用範囲も広い。
数多くの組み合わせの中から,ある条件を満たすものを見つけたり, 評価値のもっとも良いものを見つけたりする問題を考えよう。 問題の構造を解析して,方程式を解くような解法があればよいが, そうではなく, 解の候補になりうるものを片端から調べ上げる以外に手がない場合がある。 このようなときに,役に立つなアルゴリズムがバックトラック法である。
ほとんどの組み合わせ的な問題においては,解をもとめるための方程式は存在せず, バックトラック法が唯一の解法であることが多い。
8クイーン問題と呼ばれるパズルを例にとって,バックトラック法の考え方を説明する。
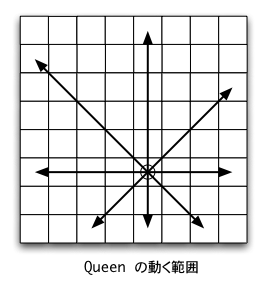
まず,チェスのクイーンの駒が動ける範囲を解説しよう。クイーンは,次の図のように自分の場所から縦横斜めの方向に何マスでも動くことができる。

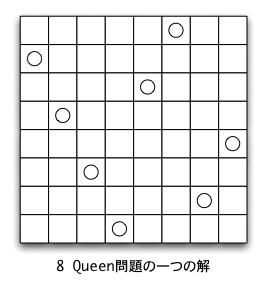
8クイーン問題とは,「8×8のチェス盤上にクイーンを8個置き, どのクイーンからも他のクイーンの場所に1手では行けないような配置にせよ」という問題である。 次図はその一つの解である。
8クイーン問題を解く方法として,まず考えられるのは,8個のクイーンの置き方をすべて調べて,条件を満たすものを探す,というものがある。 しかし,8個のクイーンをチェス盤上に置く置き方が 64C8 = 4426165368 通りあることを考えると, この方法があまりにも非現実的であることが分かる。
しかし,1つの行には1個のクイーンしか置けないことを考えると,調べる場合の数を減らすことができる。 すなわち,8つの行それぞれに,1個のクイーンをどこに置くか,ということを考えればいいから, その場合の数は, 8の8乗 = 16777216 通りである。
この考え方で解を求めるプログラムを書くと,次のようになる。
#include <stdio.h>
#define B 8
int check(int i, int j, int k, int l, int m, int n, int o, int p)
{
return (i != j) && (i != k) && (i != l) && (i != m) && (i != n) && (i != o) && (i != p)
&& (j != k) && (j != l) && (j != m) && (j != n) && (j != o) && (j != p)
&& (k != l) && (k != m) && (k != n) && (k != o) && (k != p)
&& (l != m) && (l != n) && (l != o) && (l != p)
&& (m != n) && (m != o) && (m != p)
&& (n != o) && (n != p)
&& (o != p)
&& (abs(i - j) != 1) && (abs(j - k) != 1) && (abs(k - l) != 1) && (abs(l - m) != 1)
&& (abs(m - n) != 1) && (abs(n - o) != 1) && (abs(o - p) != 1)
&& (abs(i - k) != 2) && (abs(j - l) != 2) && (abs(k - m) != 2) && (abs(l - n) != 2)
&& (abs(m - o) != 2) && (abs(n - p) != 2)
&& (abs(i - l) != 3) && (abs(j - m) != 3) && (abs(k - n) != 3) && (abs(l - o) != 3)
&& (abs(m - p) != 3)
&& (abs(i - m) != 4) && (abs(j - n) != 4) && (abs(k - o) != 4) && (abs(l - p) != 4)
&& (abs(i - n) != 5) && (abs(j - o) != 5) && (abs(k - p) != 5)
&& (abs(i - o) != 6) && (abs(j - p) != 6)
&& (abs(i - p) != 7);
}
main()
{
int i, j, k, l, m, n, o, p;
for (i = 0; i < 8; i++) {
for (j = 0; j < 8; j++) {
for (k = 0; k < 8; k++) {
for (l = 0; l < 8; l++) {
for (m = 0; m < 8; m++) {
for (n = 0; n < 8; n++) {
for (o = 0; o < 8; o++) {
for (p = 0; p < 8; p++) {
if (check(i, j, k, l, m, n, o, p)) {
printf("%d %d %d %d %d %d %d %d/n", i, j, k, l, m, n, o, p);
}
}
}
}
}
}
}
}
}
}
このプログラムはお世辞にもうまいとは言えないが, 最近のパソコンがあまりにも高速になったため,この程度のプログラムでも, 8クイーン問題の解を数秒以内に求めることができるようになってしまった。
そこで,8クイーンを拡張して,N×Nの盤上にN個のクイーンを並べる,Nクイーン問題というものを考えよう。ここで,Nが何であるかは後で定めることとする。
この問題は,本質的に上のようなプログラムではとくことができない。なぜなら, for ループがN重になるからである。 Nがプログラムを書く前に定まっていなければ,そのような for ループが書けるわけがない。
for ループが何重になるか分からないようなプログラムを書く一つのテクニックに, 関数の再帰呼び出しを用いる方法がある。それを用いたプログラムは次のようになる。
#include <stdio.h>
#define N 10
void printQueen(int queen[N])
{
int i;
printf("%d queen : ", N);
for (i = 0; i < N; i++) {
printf("%d ", queen[i]);
}
printf("\n");
}
int check(int queen[N])
{
int i, j;
for (i = 0; i < N-1; i++) {
for (j = i+1; j < N; j++) {
if (queen[i] == queen[j] || abs(queen[i] - queen[j]) == j - i) return 0;
}
}
return 1;
}
void setQueen(int queen[], int i)
{
int j;
if (i == N) {
if (check(queen)) printQueen(queen);
return;
}
for (j = 0; j < N; j++) {
queen[i] = j;
setQueen(queen, i+1);
}
}
main()
{
int queen[N];
setQueen(queen, 0);
}
このプログラムでは, N はクイーンの数(すなわち盤のサイズ)を表し,
盤上の i 行目のクイーンの位置は queen[i] で表されている。
setQueen(queen, i) は i 番目のクイーンの位置を決めて queen[i] の値を設定した後,
setQueen(queen, i+1) を呼び出している(再帰呼び出し)。
setQueen の引数 i の値は,再帰呼び出しが行われるたびに1ずつ増える。
setQueen(queen, N) のときには, queen[0] から queen[N-1] にN個のクイーンの位置が
入っているので, check(queen) で条件を満たしていることを判断している。
このプログラムは,クイーンの個数を 10 として計算を行っている。 実際に実行してみると,一つの解を出すのに,数秒あるいは数十秒かかっている。
そこで,より高速に解を求めるために,バックトラック法を用いてみる
バックトラック法は,「手を進められるだけ進めて,それ以上は無理 (それ以上進めても,解はない)ということが分かると,一手だけ戻って,やり直す」 という考え方で,全ての手を調べる方法である。
Nクイーン問題ならば,「クイーンを一つずつ置いて行き, これまでに決めたクイーンの位置からでは解は見つからないことが判明した時点で, 一つ手前に決めたクイーンの位置を,違う位置に変更して,また次のクイーンを置いていく」 という方法になる。
この「クイーンを一つずつ置いて行く」方法であるが, それまでに置いたクイーンの位置から「次のクイーンを置くことができない位置」 が定まるから,それをあらかじめ計算しておくと,処理が早くなることが予想できる。 そこで,盤の状況を表す2次元行列 board を用意して, i 行 i 列の場所にはクイーンを置くことができるかどうかを, board[i][j] の値で表すことにする。 クイーンを一つ置くごとに,そのクイーンが動いて行ける場所の board[i][j] の値を,クイーンを置くことができないことを意味する値にするわけである。
実際には,board の初期値は全部0にしておいて, 置いたクイーンから縦横斜めの方向にあるマス目の board[i][j] の値を 1だけ増やしている。 以前に置いたクイーンを取り除くときには,そのクイーンから縦横斜めの方向にあるマス目の board[i][j] の値を1だけ減らせばよい。 この両方の操作を行うのが changeBoard である。 board[i][j] の値が0であるときだけ,そこに新しいクイーンを置くことができる。
#include <stdio.h>
#include <string.h>
#define N 10
void printQueen(int queen[N])
{
int i;
printf("%d queen : ", N);
for (i = 0; i < N; i++) {
printf("%d ", queen[i]);
}
printf("\n");
}
/* (i,j)の位置から縦横斜めの方向にある board のすべての要素の値に dを加える */
void changeBoard(int board[N][N], int i, int j, int d)
{
int k;
for (k = 0; k < N; k++) {
board[i][k] += d; /* 横方向 */
board[k][j] += d; /* 縦方向 */
}
if (i > j) {
for (k = 0; k < N-(i-j); k++) {
board[k+(i-j)][k] += d; /* 右下がり斜め方向 (i > jのとき) */
}
} else {
for (k = 0; k < N-(j-i); k++) {
board[k][k+(j-i)] += d; /* 右下がり斜め方向 (i <= jのとき) */
}
}
if (i+j < N) {
for (k = 0; k <= i+j; k++) {
board[i+j-k][k] += d; /* 左下がり斜め方向(i +j < Nのとき) */
}
} else {
for (k = i+j-N+1; k < N; k++) {
board[i+j-k][k] += d; /* 左下がり斜め方向(i+j >= Nのとき) */
}
}
}
/* i 行目のクイーンの位置を設定して, setQueen(queen, board, i+1) を呼び出す
ただし, i == N のときは,一つの解が queen に入っているのでそれを表示するだけである */
void setQueen(int queen[N], int board[N][N], int i)
{
int j;
if (i == N) { /* 解が見つかった */
printQueen(queen);
return;
}
for (j = 0; j < N; j++) {
if (board[i][j] == 0) { /* (i,j) の位置に置けるならば */
queen[i] = j; /* (i,j) の位置にクイーンを置く */
changeBoard(board, i, j, +1); /* (i,j) から縦横斜めの方向のboard値を+1する */
setQueen(queen, board, i+1); /* i+1 行目のクイーンの位置を決める */
changeBoard(board, i, j, -1); /* (i,j) から縦横斜めの方向のboard値を元に戻す */
}
}
}
void findSolution()
{
int queen[N];
int board[N][N];
memset(board, 0, sizeof(board));
setQueen(queen, board, 0);
}
main()
{
findSolution();
}
memset(ptr, c, n) はポインタ ptr が指す場所から n バイトの値を c に設定する。 バイト単位で設定するので,int 型配列の初期化には向かないが, 0 に初期化するときには使用できる。
バックトラック法を関数 set の再帰呼び出しで書いたときの基本的な書き方を整理して表すと,次のようになる
set(解を入れるもの(i-1番目までは設定済み),現在の状況, 今回設定する場所 i)
{
if (i == 終わり) {
解が見つかったときの処理;
return;
}
for (今の状況において,解の i 番目の値として可能なすべての値 j に対して) {
解の i 番目の値を j として,現在の状況を表すデータを更新する;
set(今までに今の状況を表すデータ, i+1);
解の i 番目の値を j としたのを止めて,現在の状況を表すデータを元に戻す;
}
}
findSolution()
{
解を入れるものと現在の状況を表すデータを初期化;
set(解を入れるもの,現在の状況を表すデータ,0); /* 解の 0 番目の場所の設定から始める */
}
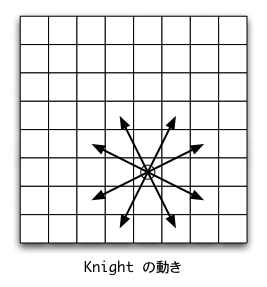
それでは演習問題として,ナイト巡回問題をバックトラック法で解いてみよう。 ナイト巡回問題とは, 「1つのナイトをチェス盤上に置き,それを動かしてチェス盤の全てのマスを通過して始めの場所に戻せ」 というものである。
ナイトの動きは,次の図で示されている。
チェス盤の大きさを変えることも考えて,それを M×N としておこう。
チェス盤の状況を表す配列 board の大きさは, ナイトが盤から飛び出してしまうことも考えて, M+4 × N+4 としておく。
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <time.h>
#define M 6
#define N 6
void printCycle(int cycle[M*N][2])
{
int i;
for (i = 0; i < M*N; i++) {
printf("(%d,%d)-", cycle[i][0]-1, cycle[i][1]-1);
}
printf("\n");
}
void backtrack(int board[M+4][N+4], int cycle[M*N][2], int n, int i, int j)
{
if (n == M * N) {
if (i == 2 && j == 2) {
printCycle(cycle);
exit(0); /* 解が1つ求まれば,プログラムを終了する */
}
return;
}
if (board[i][j] < 0) return;
cycle[n][0] = i;
cycle[n][1] = j;
board[i][j] = -1;
backtrack(board, cycle, n+1, i-2, j-1);
backtrack(board, cycle, n+1, i-2, j+1);
backtrack(board, cycle, n+1, i-1, j-2);
backtrack(board, cycle, n+1, i-1, j+2);
backtrack(board, cycle, n+1, i+1, j-2);
backtrack(board, cycle, n+1, i+1, j+2);
backtrack(board, cycle, n+1, i+2, j-1);
backtrack(board, cycle, n+1, i+2, j+1);
board[i][j] = 1;
}
void initBoard(int board[M+4][N+4])
{
int i, j;
for (i = 2; i < M+2; i++) {
for (j = 2; j < N+2; j++) {
board[i][j] = 1; /* 盤内 */
}
}
for (i = 0; i < M+4; i++) {
board[i][0] = board[i][1] = board[i][N+2] = board[i][N+3] = -10; /* 盤外 */
}
for (j = 0; j < N+4; j++) {
board[0][j] = board[1][j] = board[M+2][j] = board[M+3][j] = -10; /* 盤外 */
}
}
void findSolution()
{
int board[M+4][N+4];
int cycle[M*N][2];
initBoard(board);
backtrack(board, cycle, 0, 2, 2);
}
main()
{
findSolution();
}