「数学の世界」と「数学の拡がり」
高等学校時代に習った数学とは少し違った数学について話をします。微分や積分は使わないし、計算力は中学校程度の計算力で十分です。けれど、今まで学んできた数学と違った考え方をしなければならない部分もあるので、柔軟な思考力が要求されます。こちらの方が、本来の数学(?)に近いかもしれません。また、コンピューターを使えると、いろいろと面白いことができるかもしれません。
- オイラーとケーニヒスベルグの7橋渡り問題
次の図の一筆書きができますか? ただし、出発点に戻ってくること.
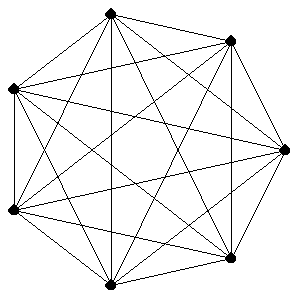
Mathematica を使うと EulerianCycle という命令で答えを出してくれます。
- オイラーの一筆書き定理
「雪の積もった公園。最も効率的に除雪車を動かすにはどうすればよいか。」
- 郵便配達員問題
「郵便配達員が、担当区域の全ての通りを通って郵便物を配達し、それから郵便局に戻ろうとしている。配達のために回る総距離を最小にするには道順をどのように決めればよいか。」
- 最短路問題とダイクストラ法
高速道路網を使って鹿児島から青森までの最短距離で行く方法。
- ハミルトングラフ
「1
匹の二十日ネズミが3×3×3の立方体の巣の中に住んでいる。この巣は1×1×1の27の立方体の部屋に分かれていて、どの部屋も隣の部屋と行き来できるようになっている。そして、各部屋には1個ずつチーズのかけらがおいてある。いまネズミが、ある隅の部屋から出発し、チーズを食べていくとする。チーズのなくなった部屋には移動できないとする。中央の部屋で食べ終わるということは可能か。」
- 騎士の巡遊問題
「チェスのナイトは一連の桂馬とびの動き方によって、チェス盤の全てのマス目を1度ずつ訪れて、もとへ戻ってくることができるか。」
- 4個の立方体(積み重ねの)問題(Instant Insanity または Irritation )
「6つの面を赤、青、緑、黄の4色に彩色された4個の立方体がある。これらを積み重ね、その際得られた(立方体4個の)”積み重ね”の四方のどの面にも、4色の色全部が現出するようにする。」
- 球面グラフ
「むかし5人の息子を持った王様がいた。遺言の中で彼は、彼の死後どの息子もそれぞれ1つの城を築き、5つの城をそのどの2つの対も交差することのない道路で連結せよと述べた。遺言の条件はみたすことができるか。」
- ドーナツ面グラフ定理
「王様の遺言はドーナツ面(RPGの主人公の住んでいる世界)上では実現される。」
- 正多面体
プラトンの多面体とも呼ばれる。正多面体は 正4,6,8,12,20面体の5種類が存在する。
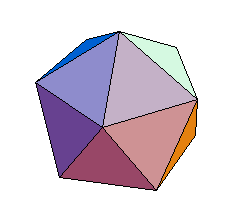
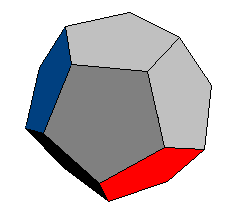
- 準正多面体
アルキメデスの多面体ともいう。「サッカーボールの形をした炭素分子。」
- 頂点の彩色と4色問題
「地球上のどんな白地図も4色で塗り分けられる。」
次の地図を隣り合った国が異なった色になるように塗り分けるには、何色必要でしょうか?
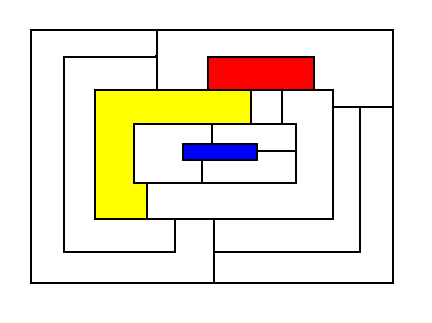
- グラフの辺の彩色とスケジューリング
「どの学生も一人一人何人かの先生と一対一の面接試験を受けなければならない。一人の先生との面接時間は一時間とする。どれだけの時間が必要とされるか。」
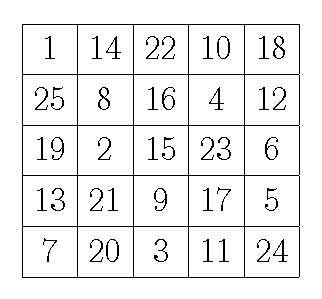
- 魔方陣
「1から25までの数を正方形に並べ、縦・横・対角線の和が全部等しくなるようする。」
- ラテン方陣
「ナンバープレイス(ナンプレ)」
- オイラー方陣
「トランプの各スーツから、それぞれの4つの数 A、K、Q、J 16枚の札を選びだし、
4×4の正方形に並べ、縦・横どの列にも同じスーツ、数が現れないようにする。」
- 完全オイラー方陣
「対角線にも同じスーツ、数が現れないようにする。」
- 完全オイラー方陣の秘密
- 時計盤算術
合同数.12=0 の算術の世界「(4+1)×3=3」.
- ディオファントス方程式
「1個79円のりんごと1個41円のミカンを6358円分買った。何個ずつ買ったのか。」
- チェックディジット
「産大学生の学生証6桁の数字をすべて加えると10で割り切れる。」
バーコードやクレジットカードのチェックディジット。
ISBN (International Standard Book Number)。
- 九去法・誤り訂正符号の原理
「321584029456447×623101487512395
=200379487114561976210025160565 は正しいか(電卓使用不可)」
- 暗号の歴史
「シーザーの使った暗号。"PBQDPHLVFDHVDU”」
- ヴィジュネル暗号
「最強の暗号はどのようにして破られたか。」
- コンピュータによる暗号作成と解読
- 公開鍵暗号と電子署名の原理




