複素力学系の世界

実力学系

• 軌道

　いま実数 x を任意に取り, 次々に2乗していくという操作を考えます． x= 2 であれば 2, 4, 16, 256, ... となります．こうしてできる数列を x の軌道といいます．極限値は x の絶対値が 1 より大のときは無限大, 1 より小のときは, 0 であることが簡単に確かめられるでしょう.

　では, 2乗してから１を引くという操作の場合はどうでしうか．ｘ＝0 であれば, 0, -1, 0, -1, ... という軌道が得られます．しかし, どういう時に収束するか, 計算によって確かめるのはなかなか骨の折れる仕事です.

• グラフによる分析

　そこで, 平面上に y = x^2 - 1 のグラフと y = x のグラフを重ねて描いて, 少し考えてみると, 軌道を簡単に見つけられることに気付くでしょう.

　このように関数や出発点を変えたときに, 軌道がどのように変化するかを調べるのは, 数学では力学系と呼ばれる分野に属しています.

複素力学系

• 充填ジュリア集合

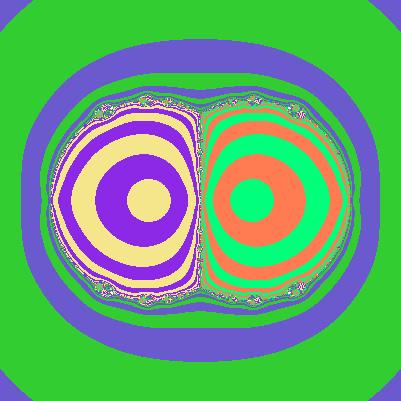
　今度は,変数を複素数zにとり, 複素数を2乗してから１を引くという操作を考えてみましょう. 複素数は平面上の点として表せますから出発点 z の軌道は平面上に点列として描かれます. 出発点 z の取り方によって様々な軌道がでてきますが, その絶対値が無限大に発散するときに, 点 z に白い印をつけ, それ以外のときには, 黒い印をつけることにして, 平面上の全ての点に対して同じことをすると, 次のような図が得られます．

　黒い部分は充填 Julia 集合と呼ばれています. 他の部分は無限大に発散するスピードに応じて色合いをかえてあります．



　また, つぎの図の黒い部分は Mandelbrot 集合と呼ばれています． Julia集合の時のように, 無限大に発散するスピードによって色合いを変えてあります．



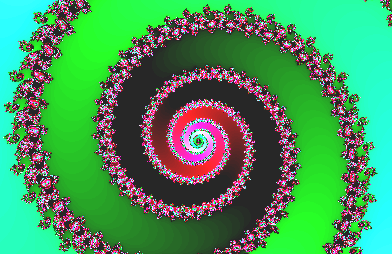
　次のはJulia 集合の一部を拡大したカラー図です.




• マンデルブロー集合

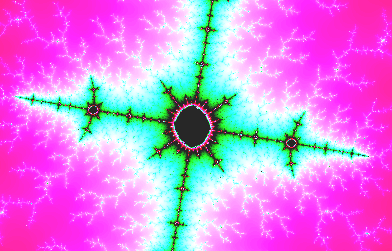
　Mandelbrot 集合の一部を拡大したカラー図です.










• ニュートン法・サーストンモデル

　以下は複素ニュートン法の理論で現れる図です． 1番目の図は３つの小さい丸の中心に z^3-1=0 の解があり、初期値によってどの解に収束するか色分けしたものです．

残りの3つはサーストンモデルとその拡大図です．